背景
前两天,师哥熬夜为群里面的同学,肝了equals和hashcode重写相关的两篇文章。今早,师哥很嚣张地到群里去吹牛了。
”
师哥:我连续两天晚上,熬夜到凌晨为亲爱的你们,写了详尽,易懂,实用性强的文章。
师哥:你们还不快去看,关注,点赞呀。
师哥:你们要是,再不去。我就把你们,都T出群了,换一批主动点的群友。
这嚣张气焰,我自己都看不下去了。但你懂的,一般装X,都会遭雷劈的。

”
师弟:师哥,我看你今天有点膨胀呀。你信不信,我分分钟,就让你又得熬个夜。
师哥:我还就不信。
师弟:师哥,为什么?System.out.println(1.0-0.1f);不等于0.9....而等于0.8999999985098839
师哥:额。。。你赢了,兄弟,你专业劈雷的吧?
师哥:我又要去熬夜了。记得晚点给我关注,点赞。
师哥:我要去熬夜写文章了。
分析
我们先来看下这段代码:
还原现场
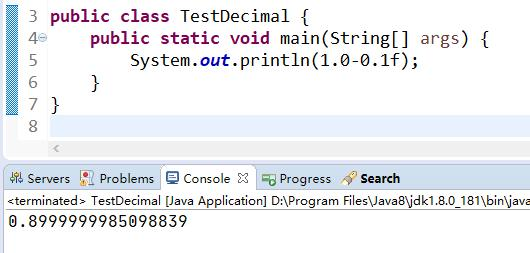
public static void main(String[] args) {
System.out.println(1.0-0.1f);
}这段代码很简单,计算1.0-0.1。我不闭眼,都知道是0.9。But。。。这段代码给我的答案,却是0.8999999985098839。
 小朋友,你是否有很多问号?
小朋友,你是否有很多问号?
师哥解答
Java语言中float与double被称为浮点数。浮点数在计算机系统中,采用科学计数法进行存储。科学计数法,是以一个有效数字(即尾数)加上幂数来表示,通常是乘以某个基数(计算机系统为2)的整数次幂得到。这种方法本身存储就是一个近似值,
所以浮点数,是无法提供完全精确的结果。它们主要为了科学计算与工程计算而生的。它们只提供较为精确的快速近似计算。在需要得到精确结果的业务场景,不能使用浮点数,比如像涉及金钱计算的银行业务等商业场景。
到底是如何存储的?
计算机只能识别二进制的0和1,那小数点要如何识别呢?一种简单的办法,将一个32位的float进行规划,前20位表示整数,后面10位表示小数部分。
但如果每个语言,各自定义一套自己的规则,那结果将不言而喻。Java语言针对浮点数存储,主要是依据于IEEE 754标准(该标准,可自行百度)。
提到标准,大家觉得必然晦涩难读的,事实也确实如此。该标准如何规定的呢?师哥自己在结合理论进行实践之后,将其概括总结为以下几点:
1.首先规定二进制小数转十进制小数算法如下(以float为例):
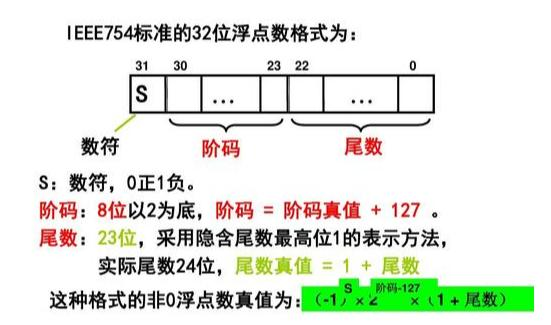
2.规定float,double各自的符号位,指数位,及尾数长度:
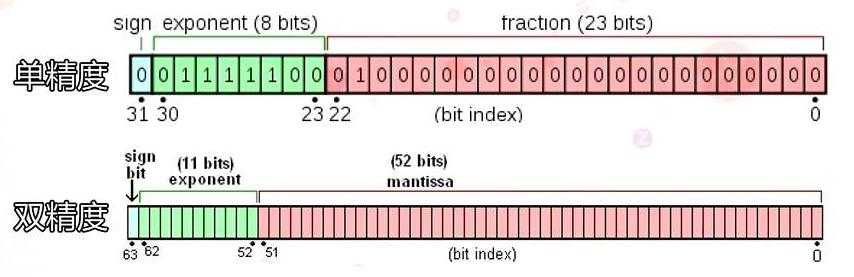
3.规定float,douoble在计算中各自的偏移量分别为127,和1023
解决
到此,我们已经知道为什么float与double计算不准确的原因了。作为一个优秀的程序员,在知道问题之后,必须要给出解决方案。师哥在此抛砖引玉,给出两个方案。
使用BigDecimal
BigDecimal类位于java.math包。其主要作用是,对大数进行精确计算。在使用BigDecimal进行计算时,下面这三个地方,需要注意。
1、不要直接使用浮点数进行对象构造。
float fnum = 0.6f; BigDecimal bigde = new BigDecimal(Float.toString(fnum));
2、BigDecimal是不可变的,每一次运算过后,需要重新对象进行存储。
public static void main(String[] args) {
BigDecimal big1 = new BigDecimal("1.1");
BigDecimal big2 = new BigDecimal("1.1");
big1.add(big2);
BigDecimal big3 = new BigDecimal("1.1");
BigDecimal big4 = big1.add(big3);
System.out.println("错误的值:"+big4);
//正确做法
BigDecimal temp = big1.add(big2);
big4 = temp.add(big3);
System.out.println("正确的值:"+big4);
}
-------------输出-------
错误的值:2.2
正确的值:3.3运用单位,拒绝浮点数
比如钱的运算,单位是元,则会有小数。我们可以将单位,设置为分即可。师哥工作如果遇到百分比,就会想办法将其转换为万分比,以此消除小数。